T1W6L3: Problem Solving with Quadratics

• Linear relationships & Quadratics §

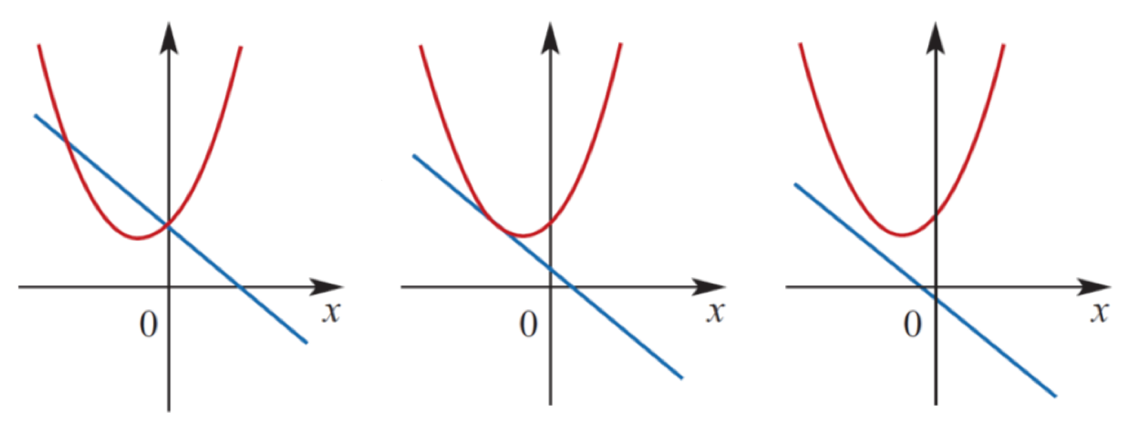
• when solving simultaneous linear and quadratic equations, you can also find either two, one or no solutions. These relationships between lines and parabolas look like:

• 

• When there is one point of intersection, the line is a tangent.

• To solve simultaneous linear and quadratic equations:

  • rearrange the quadratic to the form $y=a{x}^2+bx+c_1$
  • rearrange the linear equation to the form $y=mx+c_2$
  • equate the two solutions $a{x}^2+bx+c_1=mx+c_2$
  • rearrange and solve the resulting quadratic equation for x.
  • substitute into the linear* equation to find y

• 

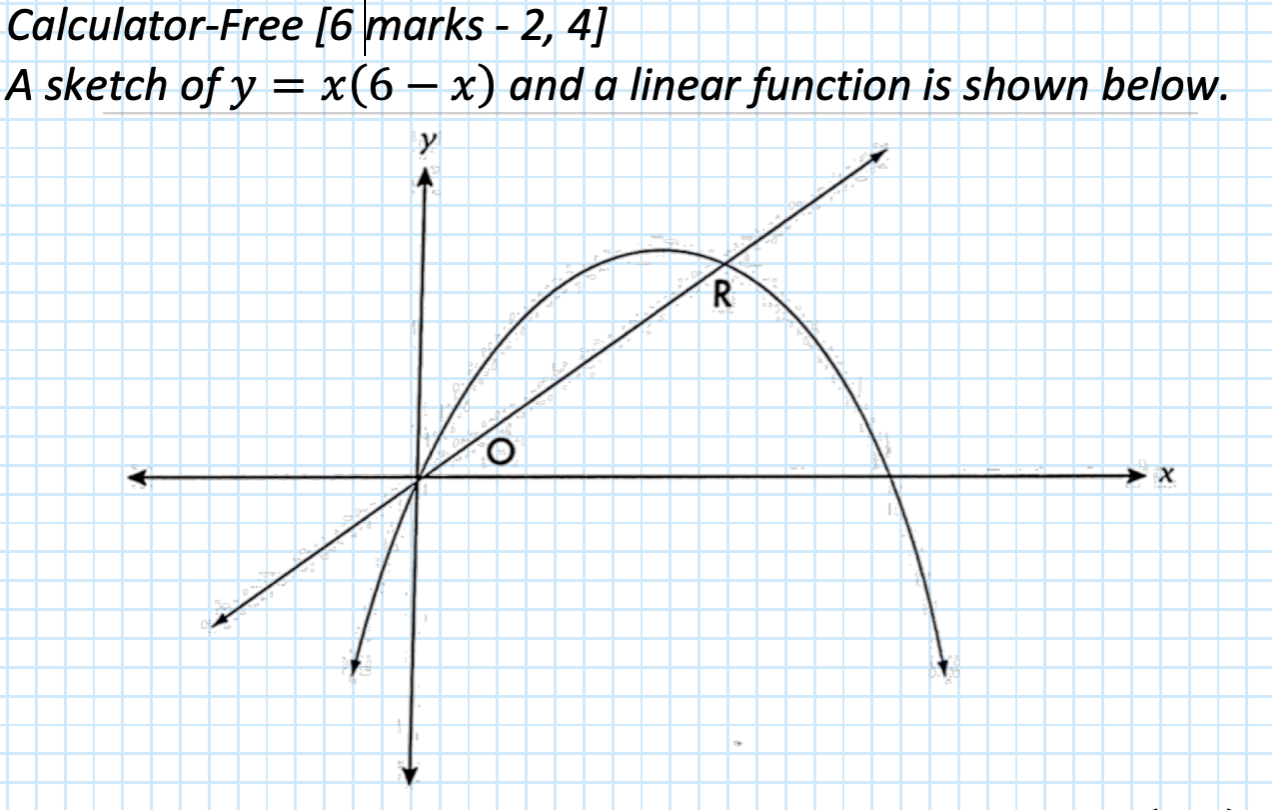
• a) the line cuts the parabola at the origin and the point R(4,r). find the value of r and the equation of the line.

  • y=4(6-4)
  • y=4(2)
  • y=8
  • R(4,8)
  • m = 8/4 = 2
  • y = 2x

• b) if the line y=mx cuts the parabola at two distinct points, find the possible values of m.

  • x(6-x) = mx
  • $6x-x^2=mx$
  • $x^2+mx-6x=0$
  • $x^2+x(m-6)=0$
  • discriminant method
    • FOR 2 SOL $\Delta >0$
    • $(m-6{)}^2-4(1)(0)>0$
    • $(m-6{)}^2>0$
    • = $m-6>0$ or $m-6<0$
    • $m>6$ or $m<6$
    • $m\ne 6$
  • other method
    • $x^2+mx-6x=0$
    • $x(x+m-6)=0$
    • $-m+6\ne 0$
    • $6\ne m$

• for no solutions

  • $\Delta =(-4m{)}^2-4(1)(20)$
  • $=6m^2-80$
  • $\Delta =0⟹16m^2-80=0$
  • $16m^2=80$
  • $m^2=5$
  • $m=\pm \sqrt{5}$

• 

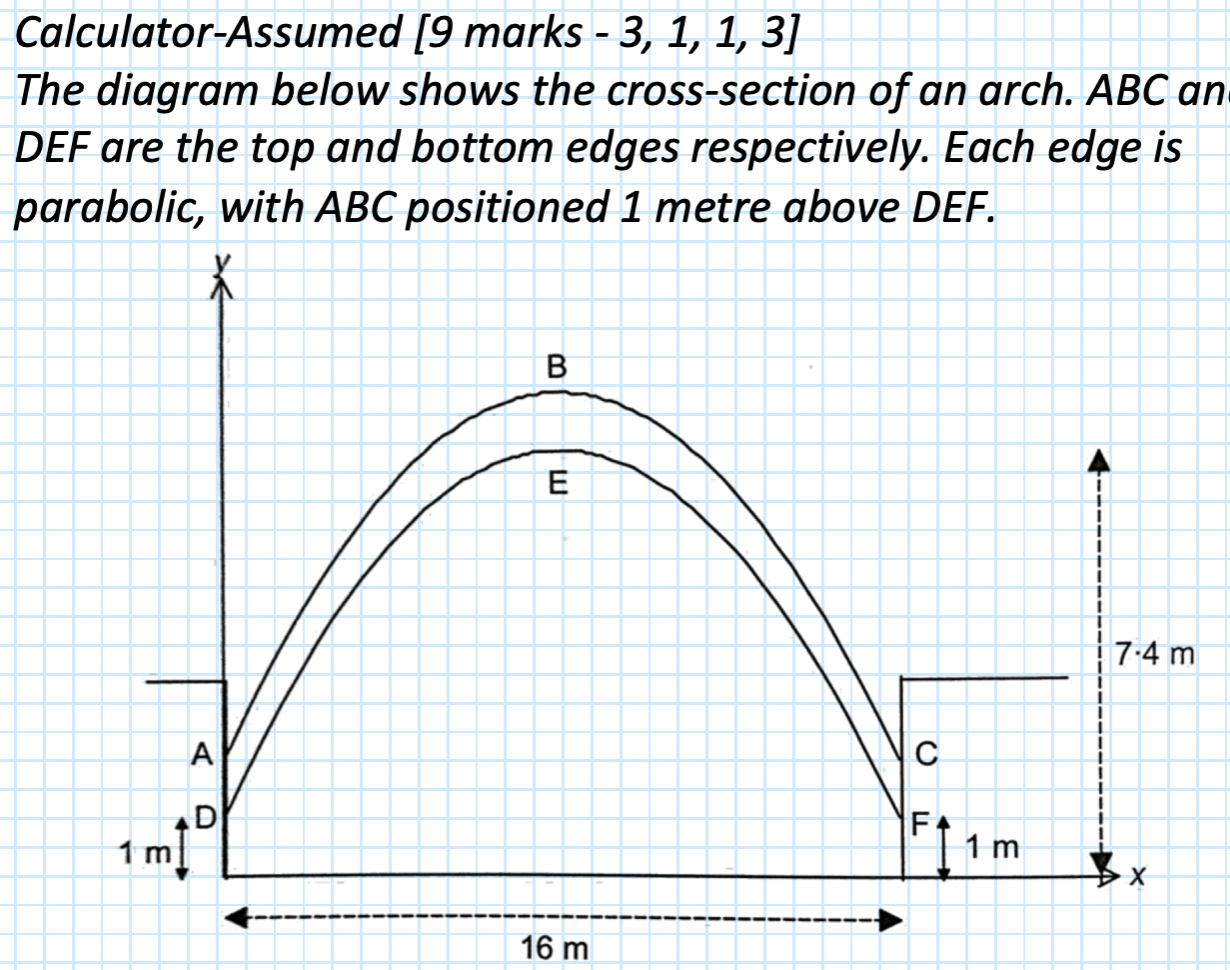
• a(x-8)^2+7.4

• SUB(0, 1)

  • 1 = a(0-8)^2+7.4
  • -6.4=64a
  • a=-0.1
  • y=-0.1(x-8)^2+7.4

• $-0.1(x-8{)}^2+7.4$

• (8, 7.4)

• $-0.1(5-8{)}^2+7.4$

• $-0.1\times 9+7.4=6.5$

• $5=-0.1(x-8{)}^2+7.4$

• $24=(x-8{)}^2$

• $\pm \sqrt{24}=x-8$

• x = 3.1, 12.9