CAP1

based on revision checklist

useful review chapters (pearson):

• 6.1: scalar vector intro
• 6.2 & 6.3: vector addition practice
• 7.1 & 7.2 & 7.4 & 7.5 & chapter review: equations of motion practice
• 7.3: recognising graphs
• 8.1: conservation of momentum
• 8.2: change in momentum
• 8.3: newtons 1st law
• 8.4: newtons 2nd law
• 8.5: newtons 3rd law
• 8.6: impulse & change in momentum
• 8 review: everything momentum and newtons laws

linear motion §

science as a human endeavour §

• understand how safety and other road users has been increased through applications of newton’s laws and conservation of momentum through helmets, seatbelts, crumple zones, airbags, safety barriers.
• this is a brief summary, and is missing a lot of detail to achieve a high mark. please revisit later.
• seatbelt designed to lock during severe deceleration.
  • as the human has the same motion applied as the car they are moving in,
  • according to newtons first law, objections in motion stay in motion: when the car stops the human keeps moving forward, and is likely to collide or be flung out.
• airbag minimises injuries
  • if vehicle impacts object at 18-20 km/h or more, airbags inflate.
  • since the body will continue to be in motion, the airbags will help decelerate the body.
• crumple zones + helmets
  • similar principles to airbags
  • helmets have like a crushable foam.
  • crumple zones extend the time for a crash to take place
• traffic safety barriers doesn’t entirely slow deceleration, but is good because it can enact an opposing force on the object, and protects people from places such as bridges.

science understanding §

scalar vs vector quantities §

• describe difference between scalar and vector quantities

• scalars §

  • values which only require the magnitude (size) and the units.
  • e.g. time is a scalar value, because it does not tell you anything about the position or direction.

• vectors §

  • values with both magnitude (size) and direction (units ofc as well)
  • examples of vectors include:
    • position
    • displacement
    • velocity
    • acceleration
    • force
    • momentum
  • because they have direction and magnitude
  • u can represent vectors as arrows
  • since arrows have direction and magnitude (length of arrow indicates magnitude and obviously direction of arrow indicates direction)
    • end of arrow is called tail, the other end is called head.
  • vector arrows in one direction is like <-> or up arrow to down arrow lmao
  • sign convention - make sure for one direction arrows (and 2 direction) say like the direction of the arrows too.

  • vectors in two directions §

    • horizontal plane (north east south west)
      • you can use true bearing or you can use quadrant bearing
      • iirc quadrant bearing is recommended for physics
      • basically N/SdegreesE/W
        • pretty self explanatory stuff
        • in words you write like from north x degrees towards the east or whatever direction lmao
    • vertical plane (up down left right)
      • i dont really want to describe and say all this shit but u get the idea
  • yeah thats basically it do the review chapter !!!

vector addition §

• how to add and subtracts vectors in two dimensions
• sometimes more than one vector can act upon an object (no way wtf?!?!?!)
  • so you need to add vectors
  • and find resultant of the two vectors.
• vectors 3d also exists but not tested ofc
• same dimension vectors are collinear (parallel)
  • so just simplify to + and - and add them together normally
• graphical method
  • use head to tail method
  • join up the tail of 1 vector to the head of another.

• two dimensions §

• head to tail method and parallelogram (not going to be bothered with parallelogram cos basically same method for same results)
• for head to tail like add the head and tail together.
  • get the angle of the shit and use trig (cosine and sine rule)
  • and calculate the hypotenuse of the angles.
  • draw it geometrically if you need help wit it
• subtracting vectors you just get the opposite vector
  • e.g. -30metres west is just 30metres east.

applications of suvat, and the equations §

please refer to my useful notes on displacement, speed and velocity and acceleration

• equations you should know applications for: $V_{avg}=\frac{s}{t},a=\frac{v-u}{t},v=u+at,s+ut+\frac{1}{2}a{t}^2,v^2=u^2+2as$ (in the formula sheet)

representations, graphs, and equations of motion §

position time graphs §

• basically y-value is position, and x-value is time.
• the gradient of the position-time graph is velocity.
  • therefore, if the graph is like linear, then velocity is constant.
  • furthermore, if the graph is quadratic-like, then velocity is changing.
    • to calculate the non-uniform velocity, the gradient will be the tangent to the point of interest 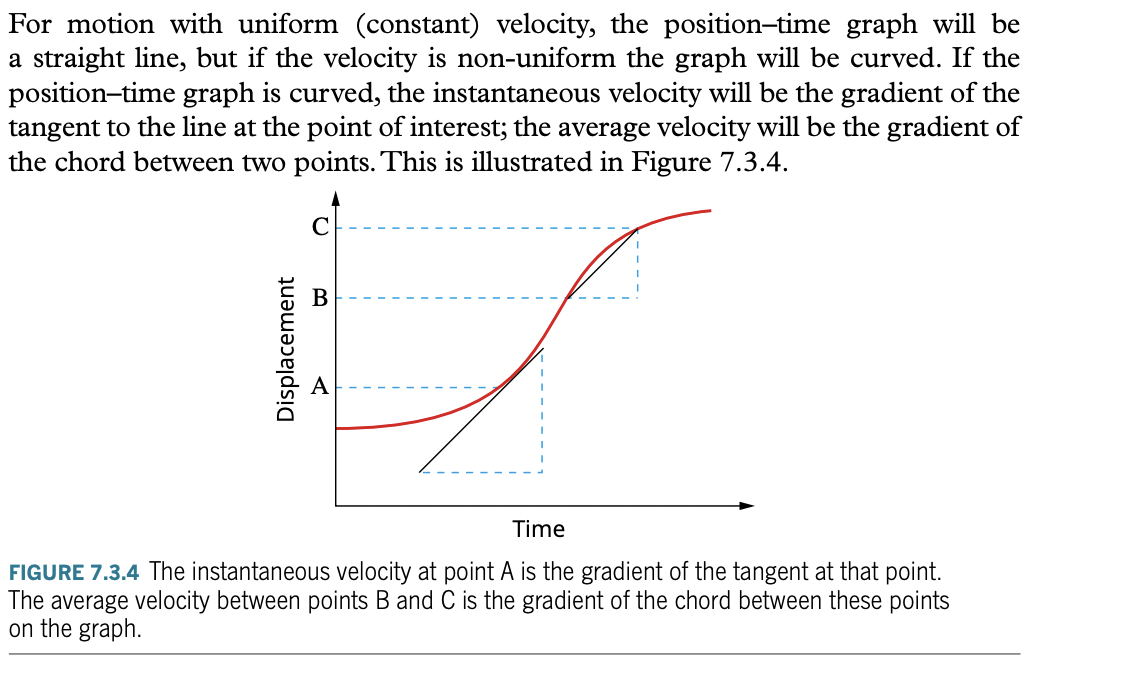(photo attached cos idk how to explain it in words!!)

velocity time graphs §

• shows how velocity of an object changes over time.
• area of a velocity graph is the displacement.
• gradient of a velocity time graph is the acceleration
• to calculate average acceleration, use $a=\frac{v-u}{t}$
• if gradient is curved and non-uniform (like position time), then acceleration non-linear. if it is uniform and linear, then acceleration is constant.

acceleration time graphs §

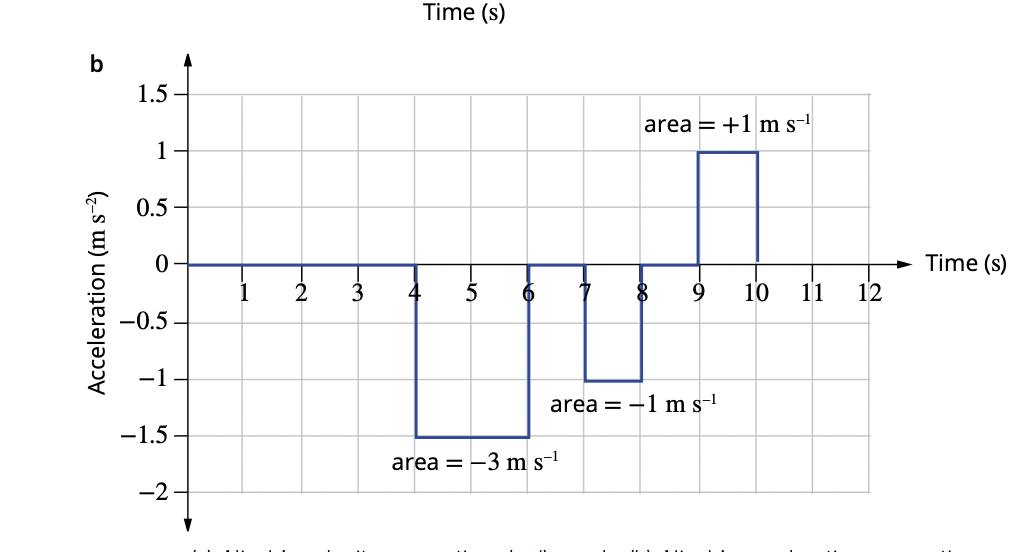illustrate the jumps with dotted lines i think is what is recommended

uniform acceleration §

• when no grah what to do?
• simple: use more precise and faster methods involving constant or uniform acceleration
• use $a=\frac{\delta v}{t}=\frac{v-u}{t}$
  • this can be rearranged to get $v=u+at$
• average velocity is $v_{avg}=\frac{s}{t}$
• since v average is half of the final - initial velocities $v_{avg}=\frac{1}{2}(v+u)$
  • $\frac{s}{t}=\frac{1}{2}(v+u)$
  • $s=\frac{1}{2}(v+u)t$ (whoa an equation of motion, derived from simple formulas)
• we know displacement is the area of a velocity time graph, which can be represented as $s=ut+\frac{1}{2}(v-u)\times t$
  • we also know that $a=\frac{v-u}{t}$
  • such $s=ut+\frac{1}{2}\times a\times t\times t=ut+\frac{1}{2}a{t}^2$

vertical motion and gravity §

• acceleration is 9.80m
• substitute for equations of motion.
• that’s it.

newton’s three laws of motion §

force preface §

force can be thought of as push or pull

• forces that directly act upon a body are called contact forces, because the force is only experienced when contact is maintained.
  • forces acted upon the body at a distance are non-contact forces.
• a force is measured in newtons

1. an object in motion stays in motion (maintain constant velocity) unless an unbalanced, external force acts upon it (the object). §

• the term maintains a constant velocity implies that, if the object is moving, then it will continue to move with a velocity that has the same magnitude and direction. e.g. a car moving 12m/s south after a set amount of time will still be moving at 12m/s (this is also consistent with zero velocity)
• unless implies an otherwise for the non-continuation of a constant velocity, and is shown through an unbalanced acting force.
• terminal velocity is the state of time when the speed a skydiver falls is equal to the air resistance, such the skydiver is unable to gain acceleration without changing anything such as mass or shape.

• inertia §

  • the law is expanded upon with inertia.
  • inertia is considered to be the resistance to a change in motion of an object.
  • as the mass of an object increases, inertia increases.
  • inertia causes:
    • harder to start moving a stationery object.
    • harder to stop moving a object with a velocity.
    • harder to change the direction of motion.
    • this can be demonstrated in real life through shopping carts.

2. force = mass x acceleration §

• connects mass, acceleration and forces
• newtons 2nd law can be edited to fit with change in momentum
• since $a=\frac{v-u}{\Delta t},F=m\frac{v-u}{\Delta t}=\frac{\Delta p}{\Delta t}$

3. every force has an equal and opposing force. §

• when hammer hits nail, the nail and the hammer both experience forces.
  • the force experienced by hammer is relative to the force experienced by the nail.
  • this observation follows newton’s third law. stating every force has an equal and opposing force.
• in a collision of a large bus and a small car, the force both experiences are the same.
  • but due to the difference in mass, one has a higher acceleration, whilst the other has a lower acceleration.
• this is true for gravity as well - called the normal force.
  • abbreviated as $F_N$ or $N$

free body diagram §

applying the relationship F=ma and Fweight=mg using free body diagrams. §

momentum §

• p=mv where p is momentum (kgm/s), m is mass of object (kg), v is velocity of object (m/s)

conservation of momentum (1d collisions) §

• $\sum p_{before}=\sum p_{after}$
• or expressed as $m_1{u}_1+m_1{u}_2=m_1{v}_1+m_2{v}_1$
  • blah blah blah yk what each variable means.
  • if the objects colliding joins together then its $m_1{u}_1+m_1{u}_2=m_3{v}_3$
  • if the objects explode and break apart into two objects then it is $m_1{u}_1=m_2{v}_2+m_3{v}_3$

change in momentum // impulse §

• $i=\Delta p=p_{final}-p_{initial}=mv-mu=m(v-u)$ (impulse is change in momentum)
• area of force time graph = momentum change = impulse (since $F=\frac{\Delta p}{\Delta t}$)

energy §

work §

• work is a measurement of how much energy to transfers forces
• measured in joules ($\frac{kg\times m^2}{s^2}$), since work is = Fs = ma x s = m x m/s^2 x s
  • since W=Fs, 1J = 1N x 1m = 1Nm
  • 1J = 1N x 1m = 1kgm/s^2 x 1m = 1kgm^2/s

energy conservation §

energy equations §

power §