Complex Numbers

Cartesian Forms (revision) §

• Not covered since this is revision.

Factorisation of Polynomials §

• A polynomial function is a sum of multiples of powers of a variable.
• e.g. $P(x)=5x^7-4x^5+3x^4-x^3+x+8$.
• The degree or the order of a polynomial (7 in the example) is the highest power of the variable.
• In the case $P(x)=3$, you can think of this as $P(x)=3x^0$, such it has the 0th degree.
• If a quadratic solution $a{x}^2+bx+c=0$ has solutions $x=p$ and $x=q$, then the LHS admits a factorisation: $a(x-p)(x-q)=0$
• i.e. solutions correspond to linear factors of the polynomials.
• this chapter extends this idea to higher degree polynomials (instead of just 2 degree ones lol)

Polynomial Arithmetic §

• Polynomials can be added or subtracted by combining like terms and simplifying.
• Polynomials can be multiplied using the distributive law
• 
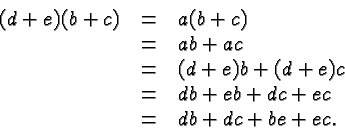
• Gets a bit complicated for division. Can be divided using polynomial division.
• 
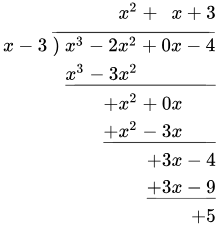
• Division with integers.
  • Consider a positive integer n (e.g. 100) and a strictly smaller positive integer p (e.g. 23)
  • 100 not divisible by 23, so there is remainder r when 100 is divided by 23.
  • Thus we can write $100=q\times 23+r$
  • q is the quotient = number of 23s in 100 :3
  • r must be smaller than divisor (23), otherwise, if it is > 23, then u did division WRONG.
• In polynomial division, the remainder isn’t always SMALLER than the divisor (like integer division). HOWEVER, the order/degree is GUARANTEED to be smaller than the divisor of the polynomial.
  • When a polynomial $P(x)$ is divided by polynomial $D(x)$, the degree of the remainder $R(x)$ will be strictly smaller than the degree of $D(x)$.
  • Thus we can write $P(x)=Q(x)D(x)+R(x)$
  • E.g. $x^4+4x^3-x+1=(x^2+5x+4)(x^2-x+1)+(-2x-3)$
  • this also works for integer division e.g. $100=4\times 23+8$
    • This can be rewritten as $\frac{100}{23}=4+\frac{8}{23}$ (wth is going on) OR $\frac{P(x)}{D(x)}=Q(x)+\frac{R(x)}{D(x)}$
    • e.g. $\frac{x^4+4x^3-x+1}{x^2-x+1}=(x^2+5x+4)+\frac{-2x-3}{x^2-x+1}$ (cannot lie idk what is going on)
• implications for algebraic fractions:
  • proper algebraic fraction: $x^2+3x+\frac{x^2+3x+4}{x^3+2x+1}$ (numerator degree is < denominator degree) - vice versa with improper algebraic fractions
• in certain later topics (partial fractions for integration) it will be necessary to rewrite improper algebraic fractions in terms of proper ones.
• We can use polynomial division to turn an improper algebraic fraction into a proper one!
  • consider

&\frac{{x^2+3x+4}}{x+4} \text{ IMPROMPER RAGE} \\ &\implies\frac{{(x-1)(x+4)+8}}{x+4} \\ &=x-1+\frac{8}{x+4}\text{ proper yay! :D} \end{align}$$ - sadler algebraic juggling ??? :P - dividing by linear (specifically) polynomials - if $P(x)$ and $(x-\alpha)$ are polynomials then $$P(x)=Q(x)(x-\alpha)+r$$ - i.e. for any polynomials $P(x)$ and $(x-\alpha)$, either $(x-\alpha)$ is a factor of $P(x)$, or there is a polynomial multiple of $(x-\alpha)$ that differs from $P(x)$ by a constant. ### The Remainder Theorem > [!note] For a polynomial $P(x)$ and a number $\alpha$, the remainder when $P(x)$ is divided by $(x-\alpha)$ is $P(\alpha)$ > e.g. $$\begin{align} &P(x)=2x^3+7x^2+10x+15 \\ \\ &P(x)=2x^3+7x^2+10x+15 \\ &P(-2)=2(-8)+7(4)+10(-2)+15 \\ &=7 \\ \\ &P(x)=2x^3+7x^2+10x+15 \\ &=(2x^2+3x+4)(x+2)+7 \end{align}$$ the remainder and the solution is the same! #### Proof $$\begin{align} &\text{Let } r \text{ be the remainder when } P(x) \text{ is divided by } (x-\alpha) \text{. Then for some polynomial } Q(x), \\ &P(x)=Q(x)(x-\alpha)+r \\ &\text{Hence, } P(x) = Q(\alpha)(\alpha-\alpha)+r=r \text{ as required} \end{align}$$ ### The Factor Theorem For a polynomial $P(x)$, $(x-\alpha)$ is a factor of $P(x)$ if and only if $P(\alpha)=0$ #### Proof Suppose $x-\alpha$ is a factor of $P(x)$. Then the remainder when $P(x)$ is divided by $x-\alpha$ is 0, Hence, by the remainder theorem, $P(\alpha)=0$. Conversely, suppose that $P(\alpha)=0$. Then the remainder when $P(x)$ is divided by $(x-\alpha)$ is 0. Hence $(x-\alpha)$ is a factor of $P(x)$. if you multiply two polynomials, the degree of the product is equal to the sum of the degrees of the polynomials. ## Other stuff which is really useful to know ### Theorem (The Fundamental Theorem of Algebra) - Every real polynomial equation of degree $n$ has exactly $n$ solutions (some of which may be repeated or complex). - Or - Every real polynomial $P(x)$ of degree $n\geq 1$ can be factorised as a product of $n$ linear factors $a(x-\alpha_{1})(x-\alpha_{2})\dots(x-\alpha _{n})$ where $a_{i}$ are the zeroes of $P(x)$. E.g. $$\begin{align} & x^4-4x^3-17x^2+110x-150 \\ & =(x+5)(x-3)(\times-(3+i))(x-(3-i)) \end{align}$$ - $\text{Suppose P(x) is a degree 7 polynomial. What is the maximum number of stationary points the grah of y=P(x) can have?}$ - derivative of degree 7 is degree 6(?) $\therefore$ Number of real distinct solutions = to 6, since real distinct solutions correlate to stationary points, P(x) has 6 stationary points. ### Theorem (Important! - part of the course) - If $z$ is a complex solution to a polynomial equation (with real coefficients), then so is $\overline{z}$. - This means that complex solutions always in conjugate pairs, so the total number of complex solutions (with non-zero imaginary part) is always even. - It also means that the total number of linear factors involving complex numbers is even - Conjugates comes as pairs, and you can ever have one solution without the conjugate pair - **What important fact does this imply about the graphs of odd degree polynomials?** - Any real polynomial equation of odd degree will have at least 1 real solutions - odd degree: starts **up**/down and finishes **down**/up - even degree: starts **up**/down and finishes **up**/down ### Theorem: Multiplicity of Factors - Suppose that $(x-\alpha)^n$ is a factor of $P(x)$. Then... - if $n$ is odd, the graph of $y=P(x)$ crosses the $x$-axis at $\alpha$ - if $n$ is even, the graph of $y=P(x)$ 'touches' but does not cross the $x$-axis at $\alpha$ - Consider $(x-2)^2(x+5)$ - both x = 2 and x = -5 is an x-axis - HOWEVER, x = 2 is a parabolic shape, whilst x = -5 - not in the scope of the syllabus, but useful knowledge which helps you be more equipped with dealing with polynomial. ## Complex arithmetic in polar form ### Polar Form of Complex Numbers - An exam question says: - Evaluate $$(2+3i)\star(1-7i)$$ - given that $\star$ could be +, -, $\times$, $\div$, you can choose the sign you use. - you would probably choose addition or subtractions, as it is easier to do than multiplication and division. - polar form is friendly for multiplication and subtraction. - reason for defining polar form is largely because it is more natural for raising powers, multiplication and division! - you can thing of additions and subtractions as a vector. - adding the complex number $1-7i$ translates the number by vector $\begin{pmatrix} 1\\-7 \end{pmatrix}$ - multiplying by pure imaginary number rotates complex number 90degrees anticlockwise. - multiplication by a pure real number dilates complex number by a factor of the pure real number. - geometric interpretation of complex number multiplication. - when multiplying by a complex number $z$ the things determining the corresponding geometric transformations are: - the distance $|z|$ from the origin (the 'magnitude' or '**modulus**') - the angle $\theta$ from the positive real axis (the '**argument**') - this suggests that a way of representing $z$ where $|z|$ and 0 are explicit could be useful! - rewrite $z=a+bi$ so that $|z|$ and $\theta$ are explicit. - **modulus** is determined using pythagorean theorem (a^2 + b^2 = c^2) - $\cos \theta=\frac{a}{|z|}, \text{ so }a=|z|\cos \theta$ - $\sin \theta=\frac{b}{|z|}, \text{ so }b=|z|\sin \theta$ - $z=|z|\cos \theta+i|z|\sin \theta$ (i is put on left hand side to avoid confusion) - $z=|z|(\cos \theta+i\sin \theta)$ $$\begin{align} & \text{e.g. the complex number } \\ & \frac{5}{\sqrt{ 2 }}+\frac{5}{\sqrt{ 2 }}i \\ & \text{ has magnitude} \sqrt{ \frac{25}{2} +\frac{25}{2} }=5 \\ & \text{and} \\ & \text{argument} \frac{\pi}{4}. \\ & \text{so it can be written as } 5\left( \cos \frac{\pi}{4} +i\sin \frac{\pi}{4} \right) \\ & \text{aka } 5 cis\left( \frac{\pi}{4} \right) \end{align}$$ - geometric interpretation of complex number multiplication. - write z = a + bi so that |z| and $\theta$ are explicit ### principal argument - the angle between the vector for $z$ and the real axis has $-\pi<\theta\leq \pi$ ## complex number (polar form) multiplication and division - abbreviated notation is $cis\theta$ which stands for $\cos \theta, i\sin \theta$ - multiplication by a complex number: - $rcis\theta \times 3cis\left( \frac{\theta}{2} \right)=3rcis\left( \theta+\frac{\pi}{2} \right)$ - number is dilated by 3 and rotated by $\frac{\pi}{2}$ - in general $r_{1}cis\alpha \times r_{2}cis\beta=r_{1}r_{2}cis(\alpha+\beta)$ - be careful when adding the angle so it is within the principal argument! ### proof $$\begin{align} \\ & \text{Claim:} \\ & \text{if }r_{1}cis\alpha \text{ and } r_{2}cis\beta \text{ are complex numbers, then} \\ &r_{1}cis\alpha \times r_{2}cis\beta=r_{1}r_{2}cis(\alpha+\beta) \\ \\ & \text{Proof:} \\ LHS &= r_{1}cis\alpha+r_{2}cis\beta \\ &= r_{1}r_{2}[(\cos\alpha i\sin \beta)(\cos\beta+i\sin \beta)] \\ &= r_{1}r_{2}[\cos\alpha \cos\beta+i\cos\alpha \sin\beta+i\sin\alpha \cos\beta+1^2\sin \alpha \sin\beta] \\ & = r_{1}r_{2}[\cos(\alpha+\beta)+i\sin(\alpha+\beta)] \\ &=r_{1}r_{2}cis(\alpha+\beta) \\ &=RHS \\ &&QED \end{align}

Regions in the Complex Plane §

this is usually the topic with the hardest exam questions - dr pearce

set notations §

• for real numbers
  • $\{x:1\le x<3,x\in R\}$
  • all values of x: such that ____ <- these conditions are true
  • transfer these concepts to the world of complex numbers.
• for complex numbers
  • $\{z:|z|=4,z\in \mathbb{C}\}$
    • wow this is a circle!
    • some people call this the locus (of |z| = 4)
  • $\{z:|z|\le 4,z\in \mathbb{C}\}$ <- now we replace = with leq sign!
    • by convention we just shade the circle in!
    • anything with modulus less than or equal to 4.
  • this can also involve the argument, rather than the modulus:
    • $\text{represent }\{z:argz=\frac{\pi }{6}\}\text{ on an Argand diagram.}$
    • note that 0+0i is excluded from the set because its argument is undefined!
    • 
  • sometimes the region represented by a set isn’t obvious. $\{z:|z+8|=|z-4i|\}$

&\text{Let } z=x+yi \\ &Then |x+yi+8| = |x+yi-4i| \\ &\sqrt{ (x+8)^2+y^2 }=\sqrt{ x^2 + (y-4)^2 } \\ &(x+8)^2+y^2=x^2+(y-4)^2 \\ &x^2+16x+64+y^2=x^2+y^2-8y+16 \\ &16x+64=-8y+16 \\ &y=-2x-6 \\ &\text{Hence, it is a straight line with a y-intercept of -6 and gradient of -2.} \end{align}$$ - Alternatively, observe that $|z-a|$ is the distance between the complex numbers $z$ and $a$ - ![[notes/images/Pasted image 20231120092819.png|400]] ## nth roots of 1 - in the real world: - $x^2=1$ solutions: $x=1$ or $x=-1$ (**2 real solutions** - 2 square roots of 1) - $x^3=1$ solutions: $x=1$ (**1 real solution** - 1 cube roots of 1) - $x^4=1$ solutions: $x=1$ or $x=-1$ (**2 real solutions** - 2 4th roots of 1) - etc... alternating - however, $x^4$ has 4 solutions (1, -1, i, -i) - you can solve this by factorising: $$\begin{align} &x^4-1=0 \\ &(x^2)^2-1^2=0 \\ &(x^2+1)(x^2-1)=0 \\ &(x^2+1)(x+1)(x-1)=0 \\ &(x-i)(x+i)(x+1)(x-1) \\ \implies &x=\pm 1 \text{ or } \pm i \end{align}$$ - consider $x^3$ $$\begin{align} & x^3=1 \\ & x^3-1=0 \\ & \text{since we know x=1 is already a solution, divide everythign by x-1} \\ & (x-1)(x^2-x+1)=0 \\ & \text{use quadratic formula to solve for x} \\ & x = \frac{1\pm\sqrt{ 3 }}{2},1 \end{align}$$ - theorem: including complex numbers,, there are $n$ $n$th roots of 1. They have modulus 1 and are spaced at angular intervals of $\frac{2\pi}{n}$ - more general theorem: given a non-zero complex number $z$, the total number of $n$th roots of $z$ (including complex roots) is $n$. - the roots all have same modulus, and are spaced at angular intervals of $\frac{2\pi}{n}$; i.e. they form the vertices of a regular $n$-gon ## powers of complex numbers (demoivres theorem) - suppose we have $-3+4i$ - we can use binomial theorem, but that is BAD, use POLAR FORM for it. 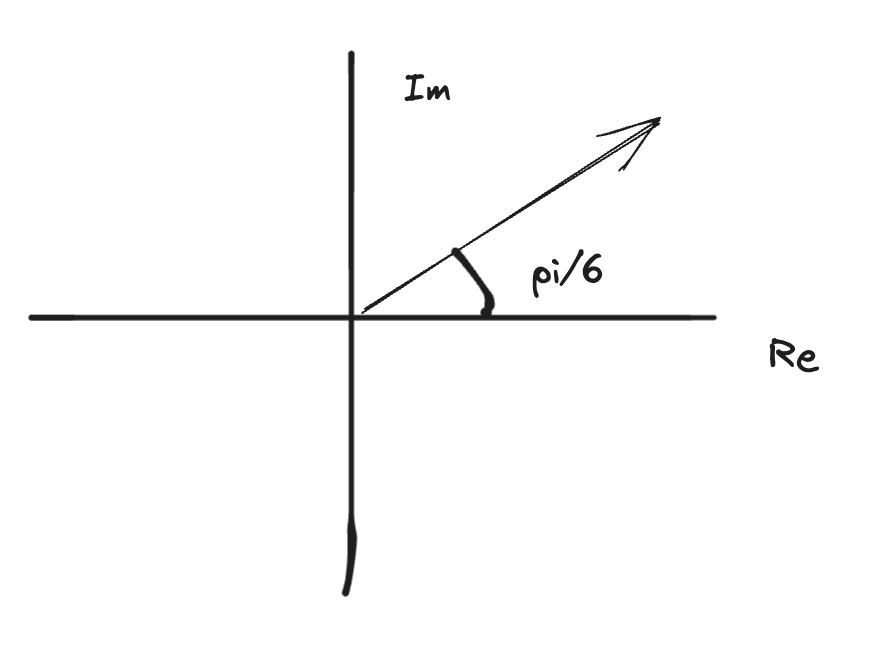- $r_{1}cis\theta \times r_{2} cis \theta_{2}=r_{1}r_{2}cis(\theta_{1}+\theta_{2})$ - for any positive integer $n$: - $(rcis\theta)^n=r^ncis(n\times\theta)$ - this leads to very important mathematical theorem: demoirves theorem ### finding $n$th roots of a complex number - find three cube roots of complex number - $z=8cis\left( \frac{\pi}{6} \right)$ - need to find all solutions to - $x^3=8cis \frac{\pi}{6}$ - $x=\left( 8 cis \frac{\pi}{6} \right)^\left( \frac{1}{3)} \right)$ - $x=2cis \frac{\pi}{18}$ - but that is only 1 solution :p - $8cis \frac{\pi}{6} - 8cis (\frac{\pi}{6} + k 2 \pi)$ infinitely many ways of representing the argument!