T1W7L1: inverse variation

recap: direct proportion §

• two quantities vary proportionately if one is always a constant multiple of the other.
• something something more goes here

inverse proportion §

• two quantities are inversely proportionate if one is always a constant multiple of the inverse of the other.
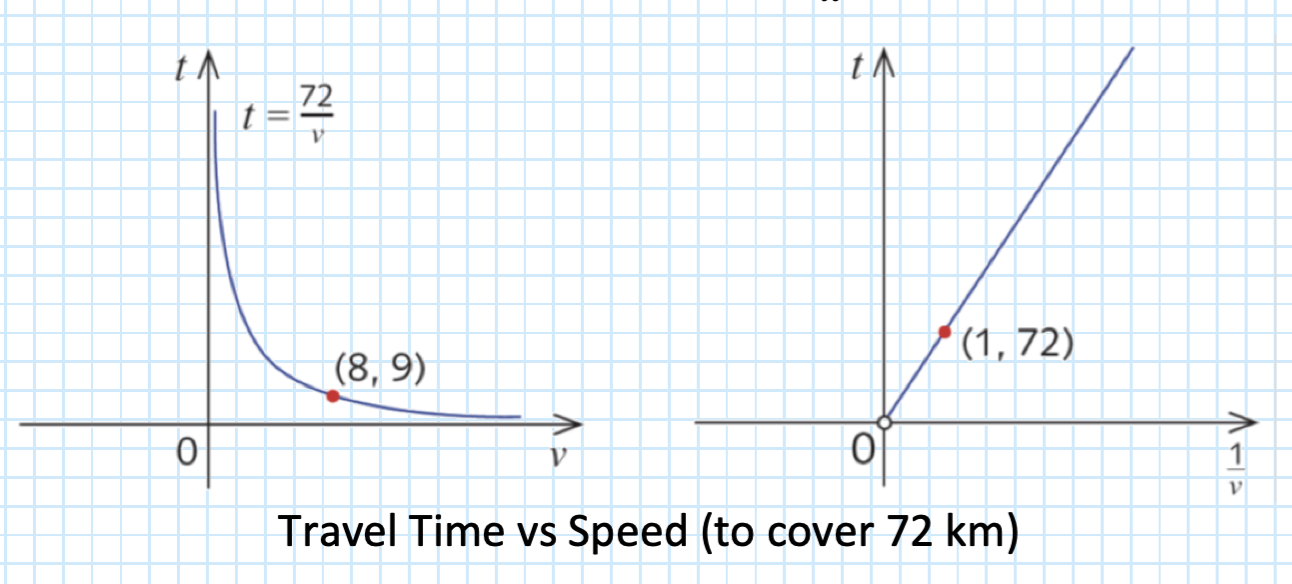
  • e.g. if you travel 72km at a constant speed, then your travel time (t hours) is inversely proportional to your speed ($v$ km/h), since t is always 72 times the inverse of $v$ (i.e. $t=\frac{72}{v}$
  • “y is proportional to $\frac{1}{x}$” can be written as: $y\propto \frac{1}{x}$
  • this can then be written as an equation as follows: $y=\frac{k}{x}$
  • where k is the constant of proportionality.
• From the equation, you can observe the following:
  • as x increases, y decreases (if k is positive), but not at a constant rate (i.e. not a straight line)
  • the constant of proportionality can be found as follows: $k=xy$
  • this can also be used as a test - if xy is constant for all (x,y), then x and y are inversely proportional.

graphing inverse proportion §

• in an inversely proportional relationship:
  • the graph of y against x is a curve called a hyperbola.
  • the graph of y against $\frac{1}{x}$ is a straight line with a gradient k that approaches the origin (excluded since $\frac{1}{x}\ne 0$)
• more generally, if $y\propto \frac{1}{x^n}$, then:
  • $y=\frac{k}{x^n}$
  • the graph of y against $\frac{1}{x^n}$ is a straight line with a gradient $k$, that approaches the origin (since $\frac{1}{x^n}\ne 0$)

practice §

• $y\propto \frac{1}{x^2}$
• $y=\frac{k}{x^2}$
• SUB ( 2, 0.1):
  • $0.1=\frac{k}{2^2}$
  • $k=0.4$
• $y=\frac{0.4}{x^2}$
• SUB X = 10
  • $y=\frac{0.4}{100}=0.004$
• SUB Y = 0.001 - $x^2=\frac{0.4}{0.001}=400$ - $x=20$
• $h=\frac{k}{r^2}$
• let $r_1=n$
• let $r_2=0.75n$
  • $h_1=\frac{k}{{r_1}^2}=\frac{k}{n^2}$
  • $h_2=\frac{k}{{r_2}^2}=\frac{k}{(0.75n{)}^2}$
    • $=\frac{k}{0.5625n^2}=\frac{1}{0.5625}\times \frac{k}{n^2}$
    • $=1.778\frac{k}{n^2}=1.778h$
    • INCREASE BY 77.8%
• SUB (4.2, 15):
  • $15=\frac{k}{4.2^2}$
  • $k=264.6$