T2W3L1: chords in circles

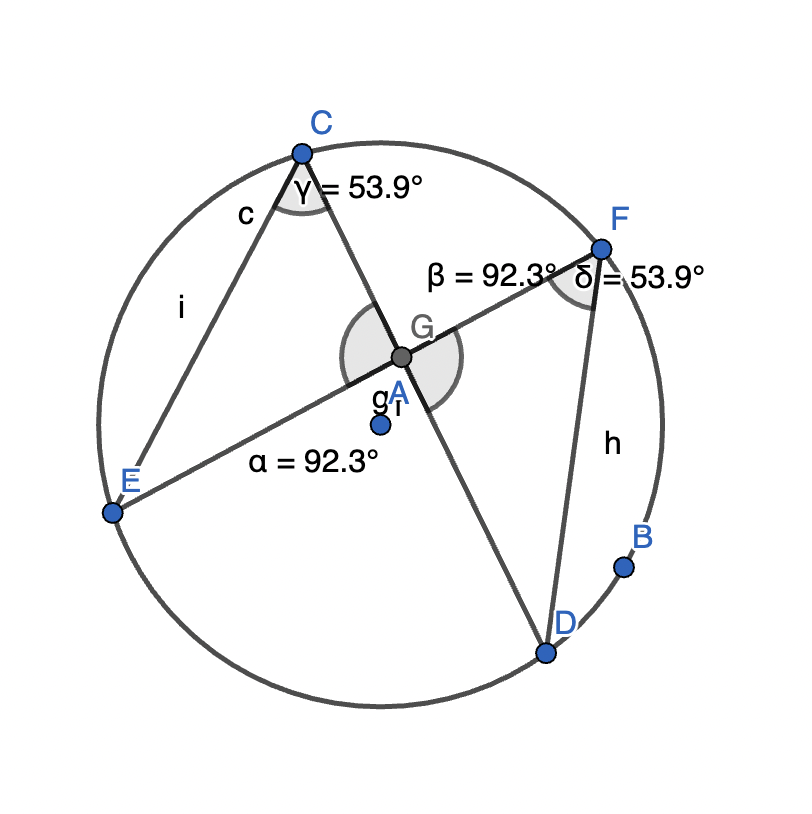
theorem 8 §

• if AB and CD of a circle that cut at a point P (which may be inside or outside the circle), then PA x PB = PC x PD.
• case 1: the intersection point P is inside the circle.
• consider triangles APC and DPB
  • $\angle APC=\angle DPB$ (vertically opposite)
  • $\angle CAB=\angle BDC$ (angles in the same segment)
• thus triangle APC is similar to triangle DPB (AAA). This gives: - $\frac{PA}{PD}=\frac{PC}{PB}$ - $\therefore PA\cdot PB=PC\cdot PD$ points are not labeled properly lmao

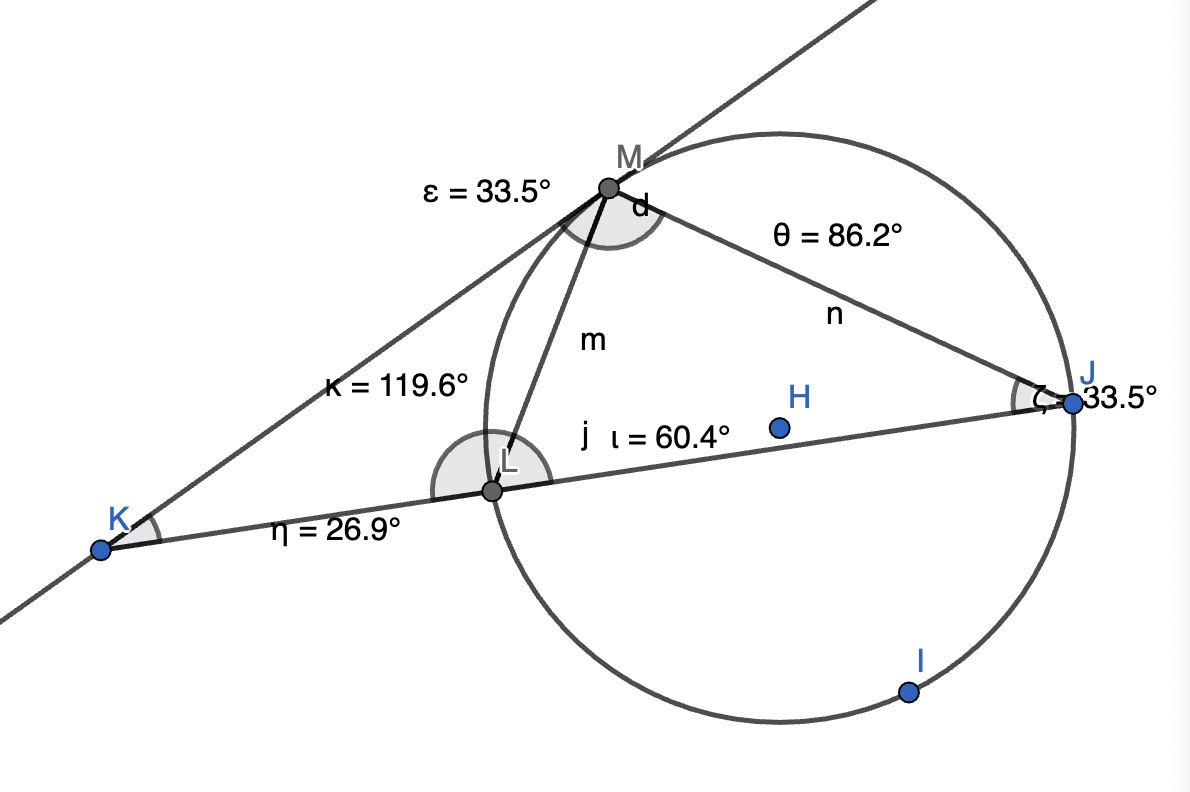
theorem 9 §

• consider triangles PAT and PTB
  • $\angle ATP=\angle TBA$ (alternate segment theorem)
  • $\angle PAT=\angle PTB$ (angle sum of a triangle)
• Therefore triangle PAT is similar to triangle PTB. (AA)
• This gives= - $\frac{PA}{PT}=\frac{PT}{PB}$ - $\therefore P{T}^2=PA\cdot PB$ points are not labeled properly lmao page 140 contains useful summaries of theorems you are expected to know you do not need to know how to prove unless a question asks for you to explain it (which may be a possibility)